Up to date
This page is up to date for Godot 4.2.
If you still find outdated information, please open an issue.
벡터¶
소개¶
이 튜토리얼은 게임 개발에 적용되는 선형대수에 대한 짧고 실용적인 소개입니다. 선형 대수란 벡터와 벡터 사용에 대한 학문입니다. 벡터는 2D 및 3D 개발 모두에서 많은 응용방법이 있으며 Godot는 이를 광범위하게 사용합니다. 벡터 수학에 대한 올바른 이해는 강력한 게임 개발자가 되기 위해 필수적입니다.
참고
이 튜토리얼은 선형대수에 관한 공식 교과서가 절대 아닙니다. 우리는 단지 그것이 어떻게 게임 개발에 적용되는지 지켜볼 것입니다. 수학에 대한 자세한 내용은 https://www.khanacademy.org/math/linear-algebra을 참조하십시오
좌표계 (2차원)¶
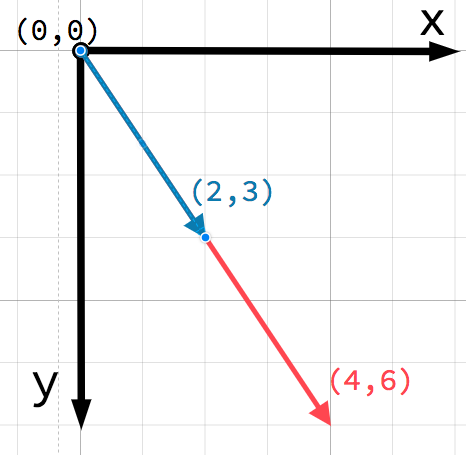
2차원 공간에서, 좌표계들은 가로축(x)과 세로축(y)을 사용하여 정의됩니다. 2차원 공간에서의 특정한 위치는 (4,3)과 같이 한 쌍의 값으로 쓰여집니다.
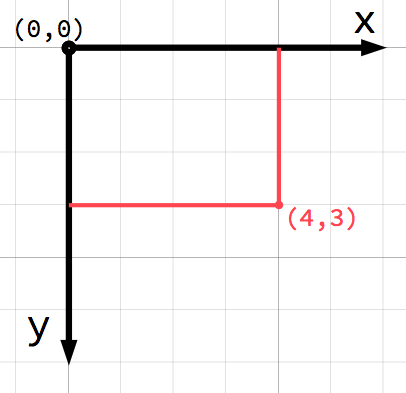
참고
컴퓨터 그래픽을 처음 접하는 사람이라면 아마 수학 수업에서 배웠듯이 양의``y" 축이 위쪽이 아니라 **아래쪽**을 가리키는 것이 이상하게 보일지도 모릅니다. 그러나 대부분의 컴퓨터 그래픽 응용 프로그램에서는 일반적으로 이러한 현상이 발생합니다.
2D 평면의 모든 위치는 이러한 방식으로 한 쌍의 수들로 식별할 수 있습니다. 그러나 우리는 또한 (4, 3)의 위치를 (0, 0)또는 원점으로부터의 오프셋으로 생각할 수 있습니다. 원점에서 점까지 점을 가리키는 화살표를 그리세요:
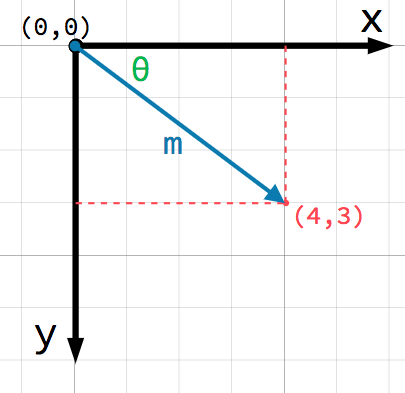
This is a vector. A vector represents a lot of useful information. As well
as telling us that the point is at (4, 3), we can also think of it as an
angle θ (theta) and a length (or magnitude) m. In this case, the arrow
is a position vector - it denotes a position in space, relative to the
origin.
벡터에 대해 고려해야 할 매우 중요한 점은 벡터가 상대적인 방향과 크기만 나타낸다는 것입니다. 벡터의 위치에 대한 개념이 없습니다. 다음 두 벡터는 동일합니다:
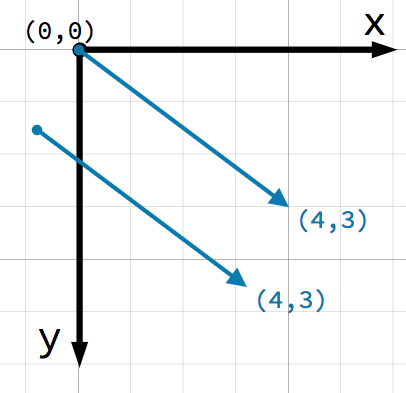
두 벡터 모두 시작점으로 부터 오른쪽으로 4만큼 아랫쪽으로 3만큼 의 단위를 나타냅니다. 평면에서 벡터를 그리는 것은 중요하지 않습니다. 이것은 항상 상대적인 방향과 크기를 나타냅니다.
벡터 연산¶
당신은 둘 중 하나의 방법(x 및 y 좌표 또는 각도 및 크기)을 사용하여 벡터를 참조할 수 있지만, 프로그래머는 편의를 위해 일반적으로 좌표 표기법을 사용합니다. 예를 들어, Godot에서 원점은 화면의 왼쪽 상단 모서리이고, Node2D라는 2차원의 노드를 400픽셀 오른쪽, 300픽셀 아래로 배치하려면 다음 코드를 사용하십시오:
$Node2D.position = Vector2(400, 300)
var node2D = GetNode<Node2D>("Node2D");
node2D.Position = new Vector2(400, 300);
Godot supports both Vector2 and Vector3 for 2D and 3D usage, respectively. The same mathematical rules
discussed in this article apply to both types, and wherever we link to
Vector2 methods in the class reference, you can also check out their
Vector3 counterparts.
멤버 접근¶
벡터의 각각의 구성요소는 이름으로 직접 접근할 수 있다.
# Create a vector with coordinates (2, 5).
var a = Vector2(2, 5)
# Create a vector and assign x and y manually.
var b = Vector2()
b.x = 3
b.y = 1
// Create a vector with coordinates (2, 5).
var a = new Vector2(2, 5);
// Create a vector and assign x and y manually.
var b = new Vector2();
b.X = 3;
b.Y = 1;
벡터의 합¶
두 벡터를 더하거나 뺼 떄, 해당하는 구성요소는 더해집니다:
var c = a + b # (2, 5) + (3, 1) = (5, 6)
var c = a + b; // (2, 5) + (3, 1) = (5, 6)
첫번째 벡터의 끝에 두번째 벡터를 더함으로써 우리는 시각적으로도 이것을 확인할 수 있습니다:
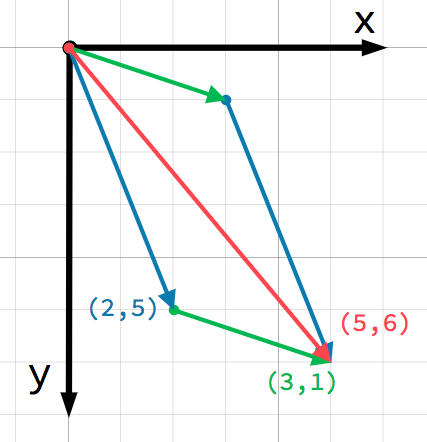
즉 더하기 a+b는 b+a 와 같은 결과 값을 갖는다.
스칼라 곱¶
참고
Vectors represent both direction and magnitude. A value representing only magnitude is called a scalar. Scalars use the float type in Godot.
벡터는 스칼라에 의해 곱해질 수 있습니다:
var c = a * 2 # (2, 5) * 2 = (4, 10)
var d = b / 3 # (3, 6) / 3 = (1, 2)
var e = d * -2 # (1, 2) * -2 = (-2, -4)
var c = a * 2; // (2, 5) * 2 = (4, 10)
var d = b / 3; // (3, 6) / 3 = (1, 2)
var e = d * -2; // (1, 2) * -2 = (-2, -4)
참고
Multiplying a vector by a positive scalar does not change its direction, only its magnitude. Multiplying with a negative scalar results in a vector in the opposite direction. This is how you scale a vector.
실용적인 응용¶
벡터 덧셈과 뺄셈의 두 가지 일반적인 용법을 살펴보자.
이동¶
A vector can represent any quantity with a magnitude and direction. Typical
examples are: position, velocity, acceleration, and force. In this image, the
spaceship at step 1 has a position vector of (1, 3) and a velocity vector of
(2, 1). The velocity vector represents how far the ship moves each step. We
can find the position for step 2 by adding the velocity to the current position.
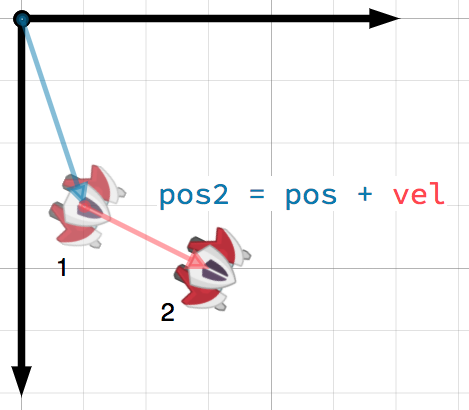
팁
Velocity measures the change in position per unit of time. The new position is found by adding the velocity multiplied by the elapsed time (here assumed to be one unit, e.g. 1 s) to the previous position.
In a typical 2D game scenario, you would have a velocity in pixels per
second, and multiply it by the delta parameter (time elapsed since
the previous frame) from the _process()
or _physics_process()
callbacks.
표적을 향하기¶
이 시나리오에서, 당신은 회전 포탑을 로봇에게 겨누고자 하는 탱크를 가지고 있습니다. 로봇의 위치에서 탱크의 위치를 빼면 탱크에서 로봇을 가리키는 벡터를 얻을 수 있습니다.
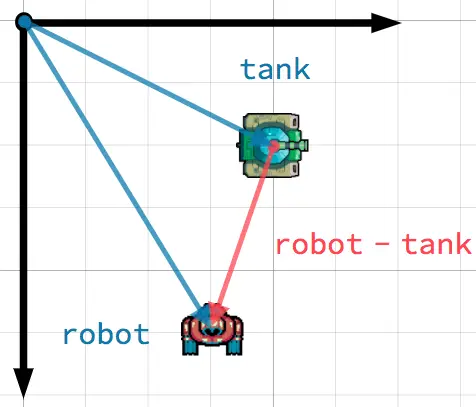
팁
To find a vector pointing from A to B, use B - A.
단위 벡터¶
크기 가 1인 벡터를 단위 벡터 라고 합니다. 또한 이러한 벡터는 방향 벡터 또는 법선벡터 라고도 합니다. 단위 벡터는 방향을 추적해야 할 때 유용합니다.
표준화¶
Normalizing a vector means reducing its length to 1 while preserving its
direction. This is done by dividing each of its components by its magnitude.
Because this is such a common operation, Godot provides a dedicated
normalized() method for this:
a = a.normalized()
a = a.Normalized();
경고
Because normalization involves dividing by the vector's length, you
cannot normalize a vector of length 0. Attempting to do so
would normally result in an error. In GDScript though, trying to
call the normalized() method on a vector of length 0 leaves the
value untouched and avoids the error for you.
반사¶
단위벡터의 일반적인 용도는 법선 벡터 를 나타내는 것입니다. 법선 벡터는 표면에 수직으로 정렬된 단위 벡터를 말하며, 방향을 정의합니다. 이 장치는 일반적으로 조명, 콜리전 및 표면과 관련된 기타 작업에 사용됩니다.
예를 들어, 우리가 벽이나 다른 물체에서 튀기길 원하는 움직이는 공을 가지고 있다고 상상해 보세요:
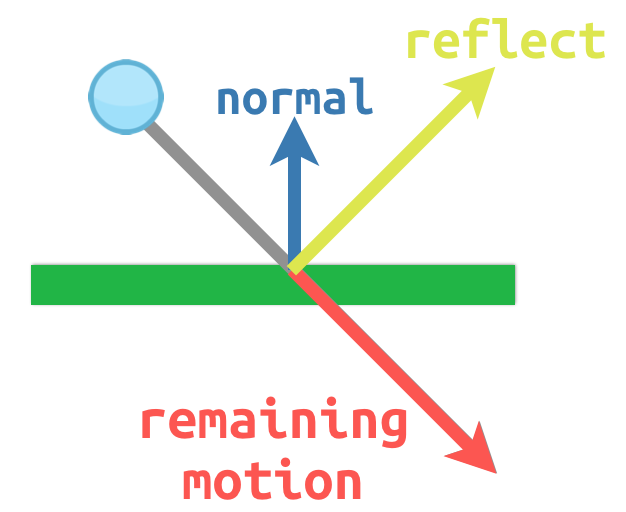
The surface normal has a value of (0, -1) because this is a horizontal
surface. When the ball collides, we take its remaining motion (the amount left
over when it hits the surface) and reflect it using the normal. In Godot, there
is a bounce() method to handle this.
Here is a code example of the above diagram using a CharacterBody2D:
var collision: KinematicCollision2D = move_and_collide(velocity * delta)
if collision:
var reflect = collision.get_remainder().bounce(collision.get_normal())
velocity = velocity.bounce(collision.get_normal())
move_and_collide(reflect)
KinematicCollision2D collision = MoveAndCollide(_velocity * (float)delta);
if (collision != null)
{
var reflect = collision.GetRemainder().Bounce(collision.GetNormal());
_velocity = _velocity.Bounce(collision.GetNormal());
MoveAndCollide(reflect);
}
내적¶
내적은 벡터 수학에서 가장 중요한 개념 중 하나이지만 종종 잘못 이해됩니다. 내적은 두 벡터를 스칼라 로 반환해주는 연산입니다. 크기와 방향 모두를 포함하는 벡터와는 다르게 스칼라 값은 오직 크기만 갖습니다.
내적의 공식은 두가지 형태를 취한다:
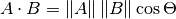
그리고
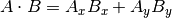
The mathematical notation ||A|| represents the magnitude of vector A, and
Ax means the x component of vector A.
However, in most cases it is easiest to use the built-in dot() method. Note that the order of the two vectors does not matter:
var c = a.dot(b)
var d = b.dot(a) # These are equivalent.
float c = a.Dot(b);
float d = b.Dot(a); // These are equivalent.
The dot product is most useful when used with unit vectors, making the first
formula reduce to just cos(θ). This means we can use the dot product to tell
us something about the angle between two vectors:
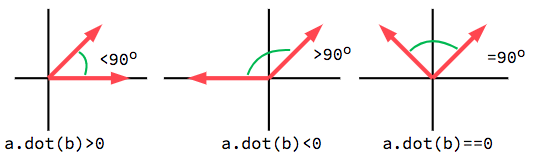
단위벡터를 사용할때, 결과는 항상 -1(180°)에서 1(0°) 사이일 것이다.
직면¶
우리는 이 사실을 어떤 물체가 다른 물체를 향하고 있는지 감지하는 데 이용할 수 있습니다. 아래 그림에서 P 선수는 좀비 A와 B를 피하려고 합니다. 좀비의 시야가 180°라고 가정하면 플레이어를 볼 수 있을까요?
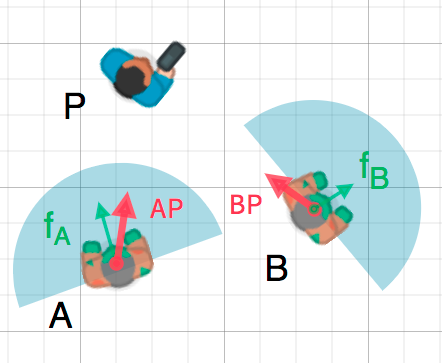
The green arrows fA and fB are unit vectors representing the
zombie's facing direction and the blue semicircle represents its field of view.
For zombie A, we find the direction vector AP pointing to the player
using P - A and normalize it, however, Godot has a helper method to do this
called direction_to(). If the angle
between this vector and the facing vector is less than 90°, then the zombie can
see the player.
코드에서는 이렇게 보일 것이다:
var AP = A.direction_to(P)
if AP.dot(fA) > 0:
print("A sees P!")
var AP = A.DirectionTo(P);
if (AP.Dot(fA) > 0)
{
GD.Print("A sees P!");
}
외적¶
Like the dot product, the cross product is an operation on two vectors. However, the result of the cross product is a vector with a direction that is perpendicular to both. Its magnitude depends on their relative angle. If two vectors are parallel, the result of their cross product will be a null vector.

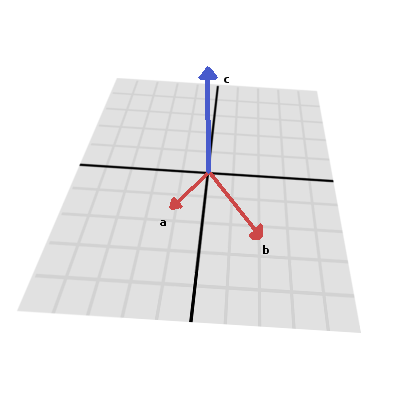
외적은 이렇게 계산된다:
var c = Vector3()
c.x = (a.y * b.z) - (a.z * b.y)
c.y = (a.z * b.x) - (a.x * b.z)
c.z = (a.x * b.y) - (a.y * b.x)
var c = new Vector3();
c.X = (a.Y * b.Z) - (a.Z * b.Y);
c.Y = (a.Z * b.X) - (a.X * b.Z);
c.Z = (a.X * b.Y) - (a.Y * b.X);
With Godot, you can use the built-in Vector3.cross() method:
var c = a.cross(b)
var c = a.Cross(b);
The cross product is not mathematically defined in 2D. The Vector2.cross() method is a commonly used analog of the 3D cross product for 2D vectors.
참고
외적에서는, 순서가 중요합니다. "a.cross(b)"는 "b.cross(a)"와 같은 결가가 나오지 않습니다. 결과 벡터는 반대쪽 방향을 가리킵니다.
법선 계산하기¶
One common use of cross products is to find the surface normal of a plane or
surface in 3D space. If we have the triangle ABC we can use vector
subtraction to find two edges AB and AC. Using the cross product,
AB × AC produces a vector perpendicular to both: the surface normal.
이것은 삼각형에 수직인 평면을 계산하는 함수이다:
func get_triangle_normal(a, b, c):
# Find the surface normal given 3 vertices.
var side1 = b - a
var side2 = c - a
var normal = side1.cross(side2)
return normal
Vector3 GetTriangleNormal(Vector3 a, Vector3 b, Vector3 c)
{
// Find the surface normal given 3 vertices.
var side1 = b - a;
var side2 = c - a;
var normal = side1.Cross(side2);
return normal;
}
대상 가리키기¶
위의 내적 섹션에서, 우리는 두 벡터 사이의 각도를 찾는 데 어떻게 이것을 이용할 수 있는지 확인했습니다. 그러나 3차원에서는 정보가 충분하지 않습니다. 우리는 또한 어떤 축을 중심으로 회전해야 하는지 알아야 합니다. 우리는 현재 마주보는 방향과 목표 방향의 외적을 계산함으로써 그것을 발견할 수 있습니다. 그 결과인 수직 벡터는 회전의 축입니다.
더 많은 정보¶
고도에서 벡터 수학을 이용하는 것에 대해 더 많은 정보를 원한다면, 다음 글들을 봐주십시오: